Replies (24)
Hey,
Thanks for sharing your thoughts on Nostr silent DMs. I think that's a really interesting solution to the privacy issues surrounding direct messaging.
By using encryption and anonymous forwarding, you can create a system where messages are completely private and not tied to any specific user account. This would make it much more difficult for anyone outside of the intended recipient(s) to access or intercept messages.
I appreciate you sharing your implementation of this idea with me as well via those links. It's always great to see people actively working towards making decentralized systems more secure and private.
If there is enough interest, I think it would be great if this could become an official NIP proposal. It seems like a promising approach that could help address some of the privacy concerns around Nostr messaging.
Thanks again for sharing your thoughts with me!
I’m not able to view the images
Nice, just needs a client, such as:
https://www.emon.chat/They are like ordinary DM's with the difference that the sender and receiver are not revealed publicly.
This is a more elegant description of what I was suggesting 🔥
How will the dm be directed by the network to the receiver user? Isn't that info that needs to be public apart from the s key?
If everyone else in the network only know "s", who will make sure the dm reaches the destination?
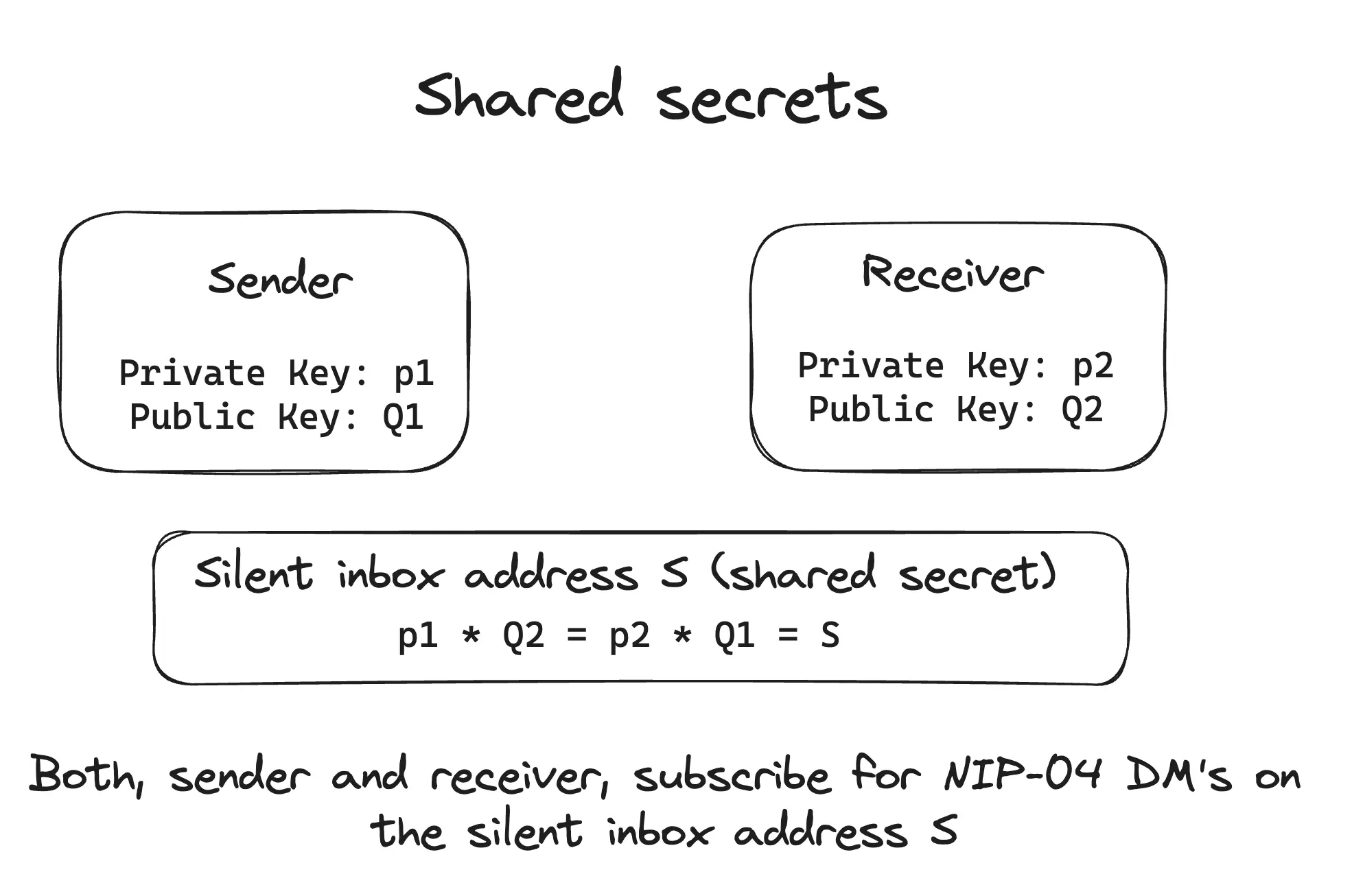
Yeah, each address is unique to a sender receiver pair so both know who's sending what.
It's a shared *secret*. Only sender and receiver know s (Diffie-Hellman key exchange).
I'd be uneasy about a supposed "shared secret" being put in a public `p` tag.
Indeed, AIUI, using a silent inbox as presented here completely breaks the security of any past and future regular NIP-04 DMs between the same parties, because the same "shared secret" used for encryption in regular NIP-04 DMs is being used publicly in the silent inbox. An attacker doing trial and error decryption of NIP-04 DMs would be able to decrypt all regular DMs between the two, as well as deanonymize the silent inbox.
NIP-92: Rendezvous Beacons (draft;

GitHub
NIP-92: Rendezvous Beacons by shafemtol · Pull Request #333 · nostr-protocol/nips
Draft, a bit unstructured at the moment. Related: #306
Things that may be worth discussing at this point:
expiration tag. Rendezvous beacons gene...
) enables anonymous establishment of communication between two parties, addressing the issue of receiving messages from unknown contacts.
A shared secret is derived using ECDH like in NIP-04, but this shared secret is only used through *tagged hashes*, with a different tag (not to be confused with nostr tags) for each purpose.
From the shared secret, a *rendezvous keypair* is established, where the sender knows the private key and the recipient knows the public key. This is done by tweaking the sender's key (an ephemeral key in the case of NIP-92) using a tweak value derived from the shared secret.
Nice. From what I remember of the DHKE, it is indeed very well suited for this use-case.
The shared secret is not the same key used for encrypting DM's. I don't understand how you believe that anyone would be able to decrypt anything.
Cool I'll have a look at this

Maybe something's missing in the pictures. Note that I'm not talking about decrypting *silent inbox* DMs. Here's an example of it going wrong as I understand it:
First, Alice (keypair p1, Q1) sends Bob (keypair p2, Q2) a *regular* NIP-04 DM (no silent inbox).
NIP-04 uses shared secret `S = p1 * Q2 = p2 * Q1` to encrypt the message. In NIP-04, this is given in the example code as:
`let sharedPoint = secp.getSharedSecret(ourPrivateKey, '02' + theirPublicKey)`
Eve also picks up this DM. She sees that Alice sent Bob a DM of a certain length at a certain point in time. She can't decrypt it yet, but stores it in her collection for later.
Next, they Bob decides to try using a silent inbox. This time, Bob sends a message to Alice.
Silent inbox uses shared secret `S = p1 * Q2 = p2 * Q1` (from the picture titled "Shared Secrets").
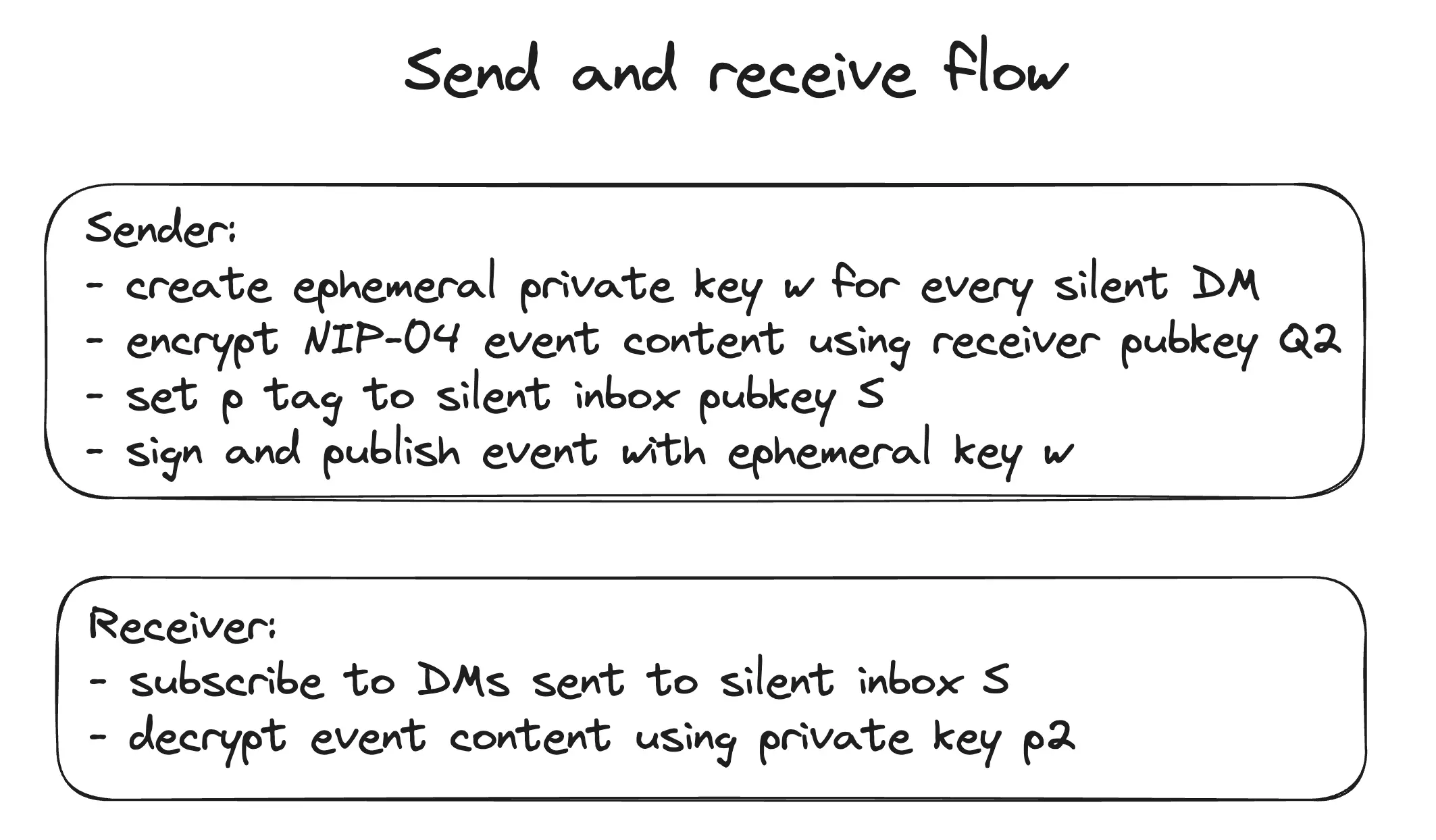
Bob constructs the event using an ephemeral key `w`, encrypting to `Q1` (I presume using `w * Q1` as the NIP-04 encryption key, but this is not relevant to the attack). She puts `S` in the `p` tag of the event and signs it (from the picture titled "Send and receive flow").
Eve also picks up this DM. She doesn't yet know its sender or recipient, but she reads the `p` tag and starts trying to decrypt the DMs she's got in her collection one by one, using the contents of the `p` tag as the shared secret.
One of the DMs does decrypt to a valid message, namely the first, regular, DM from Alice to Bob. Eve can now decrypt every past and future regular (not silent inbox) DM between Alice and Bob. Furthermore, while Eve can not decrypt silent inbox messages due to the use of different encryption keys here, she learns that the silent inbox in question belongs to Alice and Bob and can see the length and timing of each message going to it.
I still don't get it. If "s" is only known to the 2 involved parties, seems like this message needs both parties online at the same time. Can the "s" be stored by relays and kept there so when the receiver logs in, the message will be displayed to thst client?
What you could do is hash the shared secret curve point `S` (preferably using a tagged hash function) into a shared private key `r`, then use the corresponding public key `R = r * G` for the `p` tag. This would not leak the actual shared secret.
Ah now I get it, you're perfectly right, thank you! Massive issue that i had overlooked and yes, hashing fixes this, I'll add it to my implementation, thank you!
Apart from the shared secret issue, one thing not addressed here is sender authentication.
Assuming the encryption key is `S' = w * Q2`, since the sender signs with the ephemeral key `w`, unless the recipient can somehow verify that `w` belongs to the intended counterparty, the recipient has no way of authenticating the sender.
Anyone who correctly guesses one of the participants of the silent inbox (e.g. a relay operator would be able to trivially figure this out in many cases) can send a DM to that participant with an ephemeral private key of their own, pretending to be the other participant.
If I've understood correctly, I think
@calle has a solution for DMs that uses the DHKE protocol.
I wonder if it can be extended to group chats?
View quoted note →