I have been fixing renepay lately and thanks to some insightful discussions and brainstorming with René Pickhardt we have had great improvements.
In summary, the current Mininum Cost Flow algorithm (MCF) cannot allocate fees as part of the payment amount due to the sats conservation assumption that the only source and sink of flow are the sender and recipient nodes. Once fees are added on top this resulted in channels being asked to forward more sats than their probable available liquidity and consequently possibly an infinite loop of failures. To fix this we take the routes computed by the MCF and reduce their sending amount to fit all liquidity constraints:
fee, uncertainty and max_htlc; then deficit in the delivering amount is redistributed among the other routes or reallocated in a new MCF computation if necessary.
More details at this PR:  before:
before:
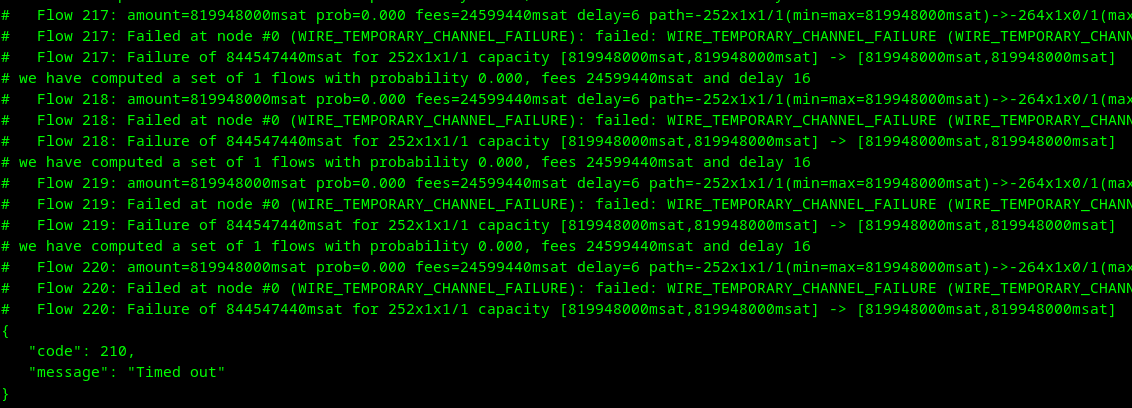 after:
after:
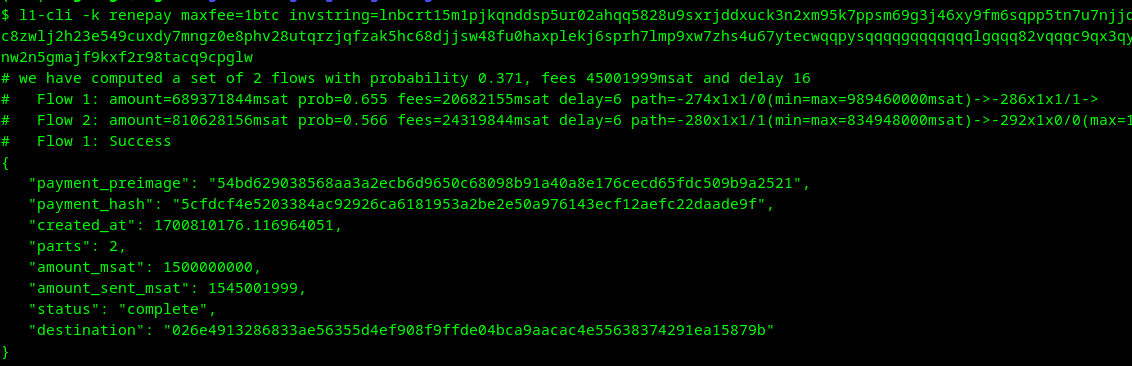
GitHub
renepay: accomodate fees in the payment flow by Lagrang3 · Pull Request #6893 · ElementsProject/lightning
Min. Cost Flow (MCF) does not resolve the correct amount in channel forwarding
because the algorithm dismisses the amounts paid as fees to the rout...
 after:
after:





